Nonlinear stabilization for Euler equations
This project is about viscous regularizations of the compressible Euler equations. The finite element discretization is stabilized using artificial viscosity operators.
Here we present some of recent numerical results. The results are obtained using nonlinear stabilization method, where the viscosity coefficient is constructed propotional to entropy and PDE residual.
To make all the features of the solution visible we often plot Schlieren gray-scale diagram of the density \(\rho\) given by
\[\sigma = \exp\left (-\beta \frac{|\nabla \rho|}{\max_{\Omega}(|\nabla \rho|)} \right),\]where \(\beta=10\).
Explosion in a closed circle with cylinders
Consider a two dimensional circle with radius \(2\) centered at the origin. Eight circular cylinders with radius \(0.3\) are placed such that their center located at \(1.4\) distance from the origin, and the distance between the neighbors are equal. A compressed gas with density 1 and pressure 1 is put inside a circle with radius \(\sqrt{0.4}\) located at the origin. The outside density is \(0.125\), pressure is \(0.1\) and velocity is at the rest. The slip boundary condition is applied to all boundaries including the cylinder boundaries.
We use rather fine mesh with relative mesh-size \(h_K\approx 0.0065\) which gives \(382\,701\) vertices and \(760\,792\) fully unstructured triangles. We use second order finite element polynomials that in total gives \(1\,539\,650\) \(\mathbb P2\) nodes. At time \(t=0\) the walls between the compressed and rested gases are taken. The circular shock is generated from the boundary of the gases and travels away from the center. After this strong shock, a circular contact line travels at the same direction as the shock but with slower speed, and a circular rarefaction wave travels towards the origin. The shock wave hits the cylinders and partially gets reflected, the other part passes between the cylinders and hits the wall of the main circle. After hitting the circle, the shock wave travels towards the origin. Again, in its way it partially gets reflected by hitting the cylinders from the other side and partially travels inward between them. On the other side, the traveling circular contact becomes weaker and at some point it rests and then travels inward towards the origin. This contact line becomes unstable and breaks downs to small vortices. The circular rarefaction wave which was traveling inwards, at some points hits the origin and reflects as a rarefaction, over-expands and creates a new shock waves traveling inwards. As time evolves this shock wave reflects from the origin and travels outward, in its way it collides with the other shock ways and contact line and so on.
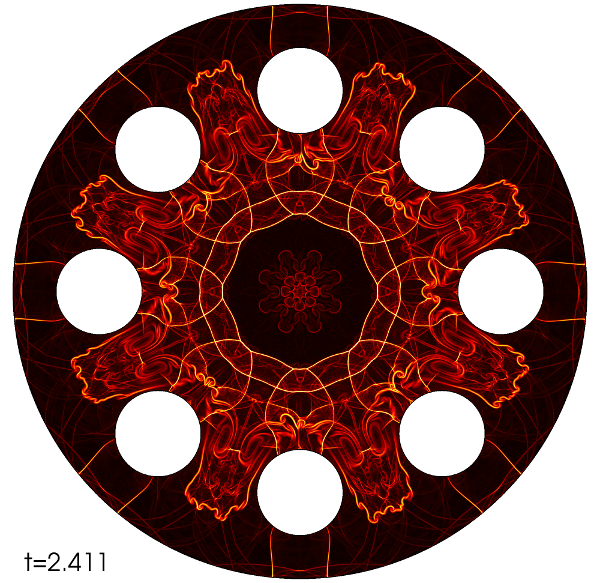

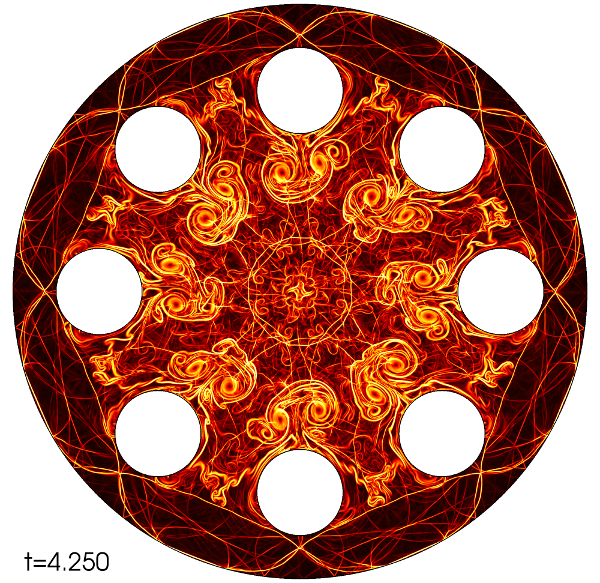
Mach 10 Double mach reflection
In this section we are interested in solving the so-called double Mach reflection problem that was popularized by Woodward and Collela in 1984. An incident Mach 10 shock wave of the ideal gas, \(\gamma=1.4\), enters to two dimensional wind tunnel with a wedge with \(30\) degree angle. Initially the value of the density is \(1.4\) and the pressure is set to 1. This problem is usually solved until \(t=0.2\). We run the computation in two meshes: a coarse mesh with mesh-size \(h_K\approx 0.025\) and a fine mesh with mesh-size \(h_K\approx 0.0025\). In both simulations second order polynomial degrees $\mathbb P2$$ are used.


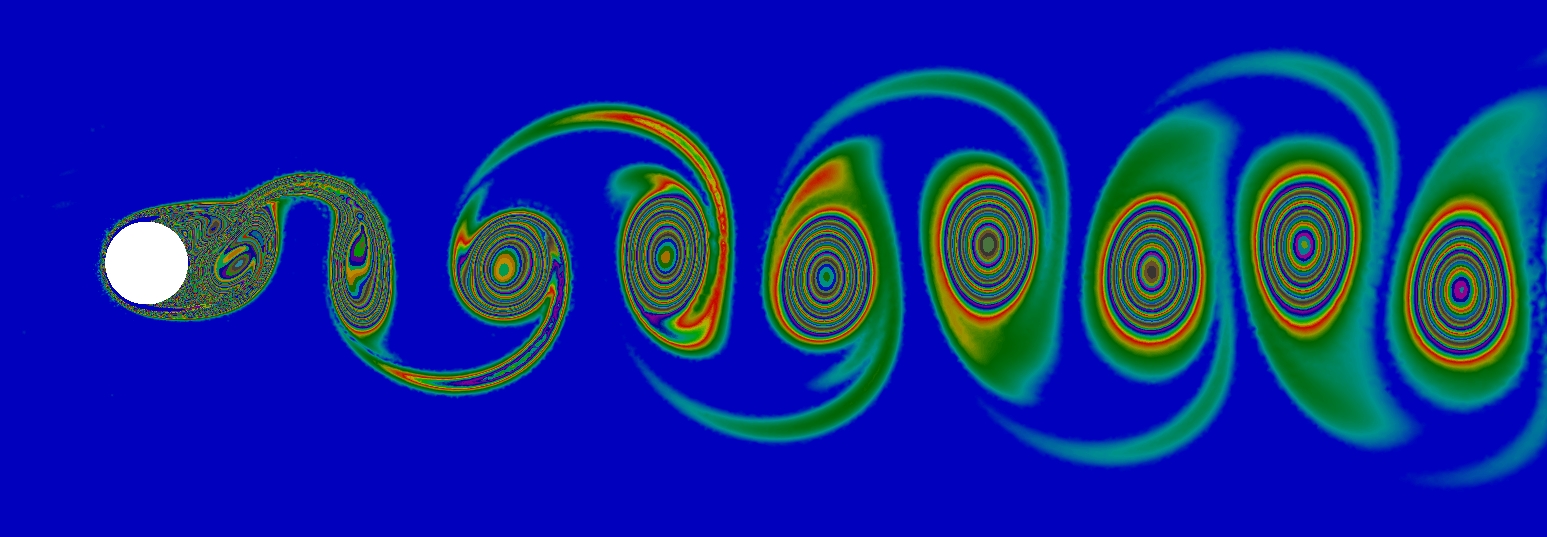
Subsonic flow, M = 0.4, viscosity = 0.0001. Vorticity
Then method can also be applied to low Mach number subsonic cases. Here is the example of a subsonic flow.
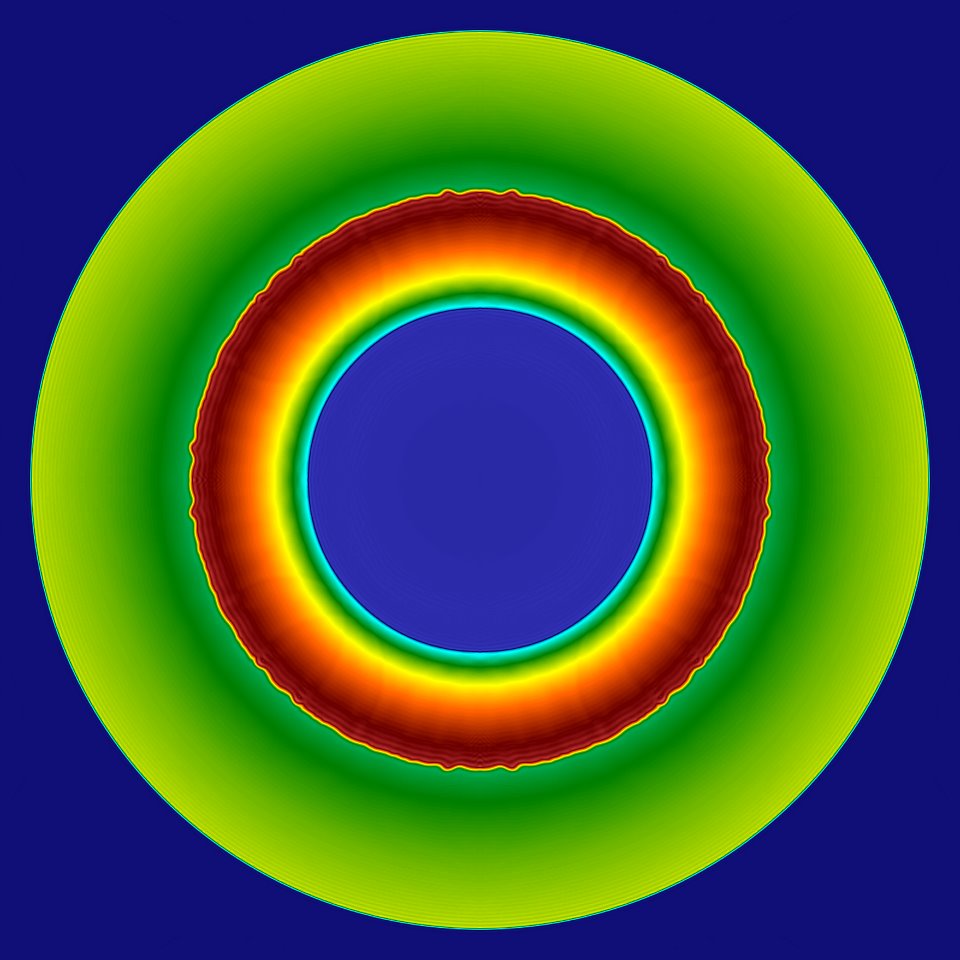
2D Riemann problem
2D Riemann problem with low density and pressure inside a circle:
\[\frac{\rho_{inside}}{\rho_{outside}} = \frac{1}{0.125}, \quad \frac{P_{inside}}{P_{outside}} = \frac{1}{0.1}.\]Color bar of density. For more information see the Computational Technology Laboratory. 640K unstructured mesh points, FEM solution with \(\mathbb P1\) elements.


Now consider the following implosion problem. The density and pressure are lower inside the rhombus:
\[\frac{\rho_{inside}}{\rho_{outside}} = \frac{0.125}{1}, \quad \frac{P_{inside}}{P_{outside}} = \frac{0.14}{1}.\]Color bar of density. For more information see the Computational Technology Laboratory. 640K unstructured mesh points, FEM solution with \(\mathbb P1\) elements.


